Mglichkeiten zur Transformation zwischen verschiedenen Koordinatenreferenzsystemen Die. Geodaeten. de. Mglichkeiten zur Datumstransformation zwischen Koordinatenreferenzsystemen. Mit der Einfhrung des Europischen Terrestrischen Referenzsystems 1. Etrs89 To Wgs84 Converter' title='Etrs89 To Wgs84 Converter' />Enhanced Tiered Storage. MarkLogic 9 adds more flexibility to the Tiered Storage feature. First, it allows documents to be matched to a tier based on a query, in. Used as graticule markings for some international maps of the British Isles Not GPScompatible. WGS84 LatitudeLongitude. Converts Direct to Postcode links to external script to do conversion Converts Direct to Approx Converts Direct to IARU Locator. Issuu is a digital publishing platform that makes it simple to publish magazines, catalogs, newspapers, books, and more online. Easily share your publications and get. ETRS8. 9 als einheitliches Bezugssystem fr die Bundesrepublik Deutschland durch die Arbeitsgemeinschaft der Vermessungsverwaltungen der Lnder der Bundesrepublik Deutschland Ad. V in den 1. 99. 0er Jahren, sind Datumstransformationen im Vermessungswesen wieder allgegenwrtig. Das ETRS8. 9 ist mit dem Internationalen Terrestrischen Referenzsystem ITRF zur Epoche 1. Da es fr die feste eurasische Kontinentalplatte definiert ist, bleibt es in sich konsistent, driftet aber gegenber dem ITRF. Fe.jpg' alt='Etrs89 To Wgs84 Converter' title='Etrs89 To Wgs84 Converter' />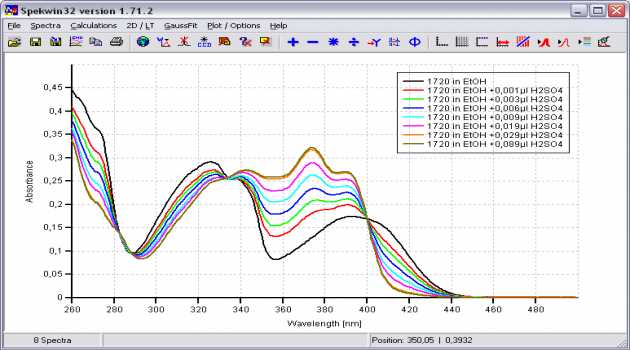Das Geodtische Referenzsystem 1. GRS8. 0 ist als Referenzellipsoid zusammen mit der UTM Abbildung fr das ETR8. Datumstransformationen sind immer dann erforderlich, wenn Koordinaten zwischen verschiedenen Koordinatenreferenzsystemen zu berfhren sind. Durch die Einfhrung vom ETRS8. Deutschland nicht nur die Abbildung ehemals 3 bzw. Gau Krger Koordinaten sondern auch das Referenzellipsoid ehemals Bessel bzw. Krassowski, sodass eine Datumstransformation zum berfhren der Koordinaten notwendig ist. Fr Deutschland relevante Referenzellipsoide sind in der nachfolgenden Tabelle zusammen mit ihren Kenngren aufgefhrt. Grundstzlich gibt es verschiedene Anstze, einen solchen Bezugssystemwechsel zu realisieren. Im Folgen sollen verschiedene Verfahren kurz vorgestellt werden. Zwei Mglichkeiten stehen als Online Transformations Tool Java. Script am Ende des Beitrags zur Verfgung. Referenzellipsoide. Ellipsoid. Groe Halbachse a mKleine Halbachse b mKrassowski. Bessel. 63. 77. 39. Hayford 1. 92. 46. GRS 8. 06. 37. 81. WGS8. 46. 37. 81. Datumstransformation mittels Helmert Transformation. Das wohl gngigste Verfahren zum berfhren von Koordinaten beruht auf einer rumlichen 7 Parameter Helmerttransformation tx, ty, tz, rx, ry, rz, m. Hierzu werden zunchst aus den verebneten Koordinaten im Startsystem geographische Lnge und Breite erzeugt. Die zweite sich anschlieende Umformung wandelt diese geographischen Koordinaten in geozentrische um. Der eigentliche Datumswechsel erfolgt schlielich mittels dieser geozentrischen Koordinaten ber eine rumliche Helmerttransformation. Aufgrund infinitesimaler Verdrehungen zwischen den Koordinatenreferenzsystemen sind hufig nur die linearisierten Transformationsgleichungen angegeben. Differentielle Helmerttransformation. Im Zielsystem knnen geographische und verebnete Koordinaten abschlieend aus den transformierten geozentrischen Koordinaten bestimmt werden. Eine schematische Darstellung aller Schritte ist der nachfolgenden Abbildung zu entnehmen. Formeln zum Umformen finden sich in der geodtischen Standardliteratur bspw. Hofmann Wellenhof et al. Stelle nicht nher errtert werden. Schematische Darstellung eines Bezugssystemwechsels mit Geo. Tra. Bei der praktischen Handhabung ist vor allem die ellipsoidische Hhe h, die beim bergang von geographische in geozentrische Koordinaten bentigt wird, problematisch, da meist die Quasigeoidhhe zur vorliegenden Normalhhe bzw. Geoidundulation bei orthometrischen Hhen unbekannt ist. Um den Einflu der Hhenkomponente auf die verebneten Koordinaten aufzuzeigen, wird nachfolgend der Beispieldatensatz 5. Ihde und Lindstrot 1. Hhen mit dem freien Programm Geo. Tra ins ETRS8. 9 transformiert. Ferner ist die Genauigkeit des Datumsbergangs durch die Qualitt der vorgegebenen Transformationsparameter limitiert. Transformation eines DHDN 1. Punktes mit variablen Hhen ins ETRS8. Resize Log File Mssql. Hhe mEast mNoth m2. Auch auf der Basis geographischer Koordinaten kann ein Systembergang erfolgen. Eine explizite Umformung in geozentrische Koordinaten entfllt dabei. Da sich die geographische Lnge und Breite jedoch direkt in geozentrische Koordinaten umformen lassen, ist diese Transformation quivalent zur oben genannten Vorgehensweise. Neben den 7 Parametern der rumlichen Helmerttransformation sind die groe Halbachse und die inverse Abplattung des Bezugsellipsoids im Startsystem a. I, f. I und Zielsystem a. II, f. II vorzugeben z. B. Heck 2. 00. 3. Ellipsoidbergang mittels Helmerttransformation mit geographischen Koordinaten. Mit den Beziehungen. Hilfsgrenerhlt man letztlich die transformierten geographischen Koordinaten. Datumsbergang. Wird Mh Nh a, e. W 1 subsituiert, gelangt man zur so genannte sphrische Approximation, bei der jedoch nur eine Genauigkeit von ca. Heck 2. 00. 3, Ihde und Lindstrot 1. Fr Deutschland relevante Transformationsparameter sind in der nachfolgenden Tabelle zusammengestellt. Mit diesen globalen Parameterstzen sind jedoch nur Genauigkeiten von 2 5m zu erzielen. Bei hheren Anforderungen sind daher lokal bestangepasste Parameter zu verwendet. Globale Parameterstze zur Datumstransformation ins ETRS8. CRS EU, Ihde und Lindstrot 1. Heck 2. 00. 3S4. S4. DHDN 1. 99. 5DHDN 2. ED5. 0tx2. 4m2. Die hufig anzutreffende Molodensky Transformation stellt letztlich eine weitere Vereinfachung der o. Gleichungen dar. Im Gegensatz zur rumlichen 7 Parameter Helmerttransformation wird der Datumsbergang hierbei lediglich durch drei Verschiebungsparameter tx,ty,tz beschrieben. Sowohl die Drehungen rx,ry,rz als auch die Mastabsabweichung m sind hierbei zu Null gesetzt z. B. Deakin 2. 00. 4. Molodensky Shift. Wird dieser Datumsshift anstelle der geographischen Lnge und Breite mit geozentrischen Koordinaten ausgedrckt, so erhlt man die deutlich kompaktere Formel. Datumstransformation mittels NTv. Gitterdaten. Eine weitere Mglichkeit zur Transformation von Koordinaten zwischen Bezugssystemen bietet das NTv. Verfahren. NTv. 2 steht fr National Transformation Version 2 und wurde Ursprnglich in Kanada entwickelt. Die Idee dieses Verfahrens basiert auf dem Ableiten von Shiftwerten aus einem regelmigen Gitter geographischer Koordinaten. Zunchst sind fr den zu transformierenden Punkt die vier Punkte der Gittermasche zu ermitteln, in der dieser liegt. Mittels bilinearer Interpolation werden die Shiftwerte fr den zu transformierenden Punktes aus den Shiftparametern der selektierten Masche bestimmt. Die Interpolation von geographischer Lnge und Breite erfolgt getrennt voneinander. Durch Addition der individuellen Shiftwerte zu den geographischen Koordinaten des Punkt im Startsystem erfolgt die berfhrung ins Zielsystem z. B. Ahrens und Bhmer 2. Bilineare Interpolation einer NTv. Masche. Im Rahmen der Bundeseinheitlichen Transformation fr ATKIS Be. TA2. 00. 7 hat die Ad. V fr die gesamte Bundesrepublik Deutschland einen NTv. Gitterdatensatz erzeugt, der geographische Koordinaten zwischen den Referenzsystemen DHDN und ETRS8. Ad. V 2. 01. 2. Die Genauigkeit der so transformierten Punkte liegt bei unter 1m. Einige Bundeslnder bieten darber hinaus eigene NTv. Gitterdaten an, mit denen hhere Genauigkeiten zu erwarten sind. Gegenber dem o. g. Bezugssystemwechsel bietet das NTv. Verfahren rechentechnisch einfach zu handhabende Formeln. Da keine ellipsoidischen Hhen bentigt werden, entfllt die o. Problematik der Geoidundulation. Online Transformation. Mit dem nachfolgenden Transformationstool knnen online Datumstransformationen zwischen dem DHDN 2. ETRS8. 9 auf dem Gebiet der Bundesrepublik Deutschland durchgefhrt werden.